MAB问题
bandit算法来源于大家熟悉的赌博学。一个赌徒,要去摇老虎机,而每个老虎机吐钱的概率不一样,他不知道老虎
机吐钱的概率分布,怎样才能收益最大化呢?这就是多臂老虎机赌博问题,简称MAB问题。
1.当推荐系统有新用户时,怎么快速地知道他对每类内容的感兴趣程度?即推荐系统冷启动问题。
2.系统中有若干广告库存物料,怎样展示,才能点击收益最大呢,是不是每次都挑最好的那个?
3.设计了新的策略或者模型,如何知道他和旧模型谁更靠谱又对风险可控呢?
这些关于选择的问题,我们都可以简化成一个MAB问题。
对于推荐系统里的两个顽疾,一个冷启动,一个探索利用,bandit算法都可以提供帮助。
bandit算法
思想:看看选择会带来多少遗憾,遗憾越少越好。在 MAB 问题里,用来量化选择好坏的指标就是累计遗憾,计算公
式如图。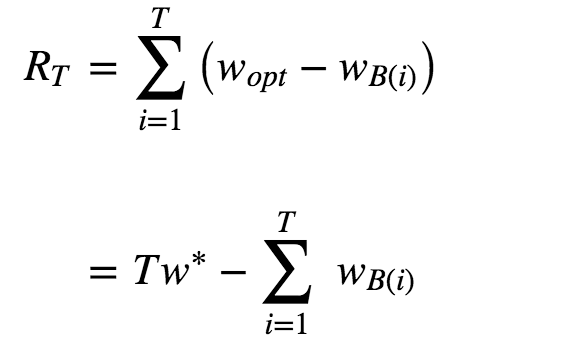
公式由两部分构成:一个是遗憾,一个是累积。求和符号内部就表示每次选择的遗憾多少。
Wopt表示选择了最好的选择获得收益,WB(i)表示实际选择得到的收益,两者之差就是遗憾的量化,T次之后,就有了
累计遗憾。
他的套路就是:小心翼翼地试,越确定某个选择好,就多选择它,越确定某个选择差,就越来越少选择它。简单说就
是,把选择的机会给“确定好的”和“还不确定的”。
bandit算法有几个关键元素:臂,回报,环境。
1.臂:每次选择的候选项,好比老虎机,有几个选项就有几个臂;
2.回报:就是选择一个臂之后得到的奖励,好比选择一个老虎机后突出的金币;
3.环境:决定每个臂不同的那些因素,统称环境。
类比推荐系统:
1.臂:每次推荐的候选池,可以是具体物品,也可以是推荐策略,也可能是物品类别;
2.回报:用户是否对推荐结果喜欢,喜欢就是正面回报,没有就是负面回报或者零回报;
3.环境:用户就是不可捉摸的环境。
汤普森采样算法
原理:假设每个臂是否产生收益,是由一个概率分布决定的,这个概率分布是贝塔分布。每次选择时,每个臂产生一
随机数,按这个数排序,产生最大随机数的那个物品为输出。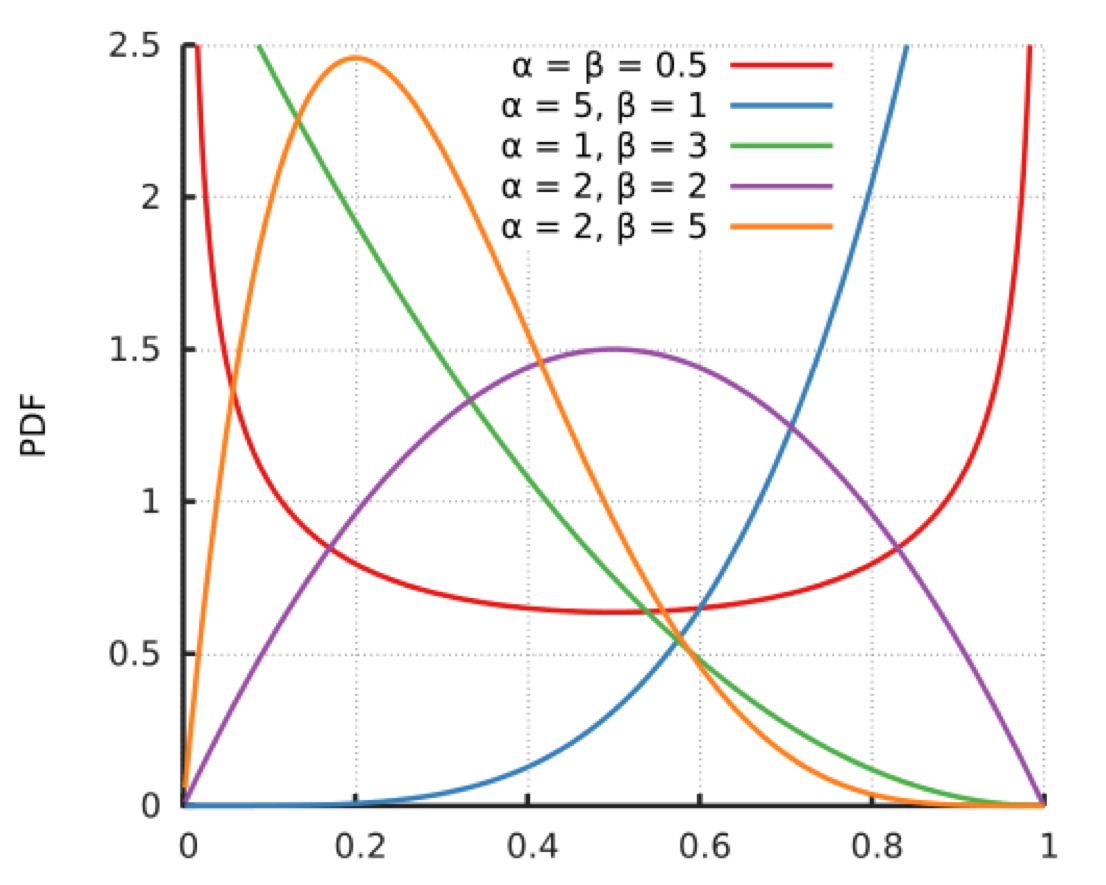
贝塔分布由两个参数a和b决定,他们决定了分布的形状和位置:
1.当a+b值越大,分布曲线越窄,分布就越集中,这样产生的随机数容易靠近中心位置;
2.当a/a+b的值越大,分布中心位置越靠近1,反之越靠近0,这样产生的随机数也相应更容易靠近1或者0.
我们可以简化成3种情况:
1.曲线很窄,而且靠近1;
2.曲线很窄,而且靠近0;
3.曲线很宽。
我们把贝塔分布的a参数看成推荐后得到用户点击的次数,把分布的b参数看成是没有得到用户点击的次数,这样就和
推荐系统联系上了。
实际使用时,要为每个用户保存一套参数,候选集有m个,用户有n个,那么就要保存2mn个参数。
UCB算法
UCB 算法全称是 Upper Confidence Bound,即置信区间上界。每次选择评分最高的候选臂输出,每次输出后观察用户
反馈,回来更新候选臂的参数。公式为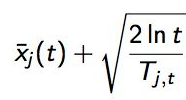
公式有两部分,加号前面是这个候选臂到目前的平均收益,后面叫做Bonus,本质上是均值的标准差,反应了候选臂效
果的不确定性,即置信区间的上边界。t是目前的总选择次数,Tjt是每个臂被选择次数。
由公式我们可知,平均收益很大,bonus大,被选择时有优势。
他的思想和汤普森采样一样:
1.以每个候选的平均收益为基准线进行选择;
2.对于被选择次数不足的给与照顾;
3.选择倾向的是那些确定收益较好的候选。
Epsilon贪婪算法
略
效果对比
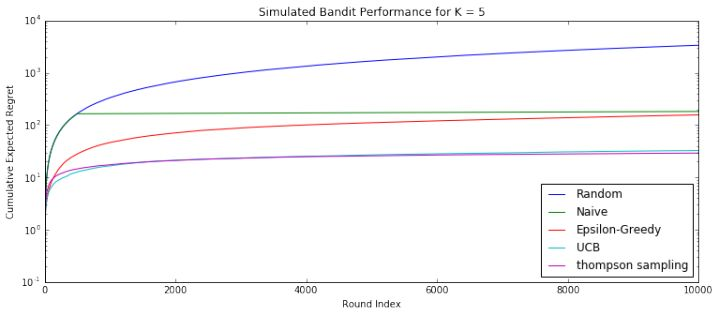
汤普森采样>UCB>Epsilon贪婪算法>朴素选择>完全随机
冷启动
冷启动问题,我们很容易想到利用Bandit算法来帮忙解决。
针对每个新用户维护k个topic,使用Bandit方式。