Unique Paths

唯一路径

题目

A robot is located at the top-left corner of a m x n grid (marked ‘Start’ in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked ‘Finish’ in the diagram below).

How many possible unique paths are there?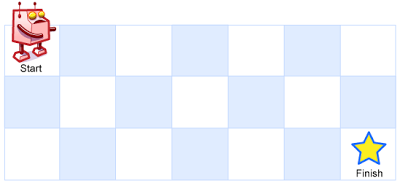

Above is a 7 x 3 grid. How many possible unique paths are there?

Note: m and n will be at most 100.

Example 1:

Input: m = 3, n = 2
Output: 3
Explanation:
From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:

1. Right -> Right -> Down
2. Right -> Down -> Right
3. Down -> Right -> Right
   Example 2:

Input: m = 7, n = 3
Output: 28

解析重点

1.这道题可以看作一道数学题，机器人总共走m+n-2步，m-1步用于向右走，因此总共路径数=C(m+n-2,m-1).
2.但是，这里我们可以把他看作动态规划的题目，以图中所示，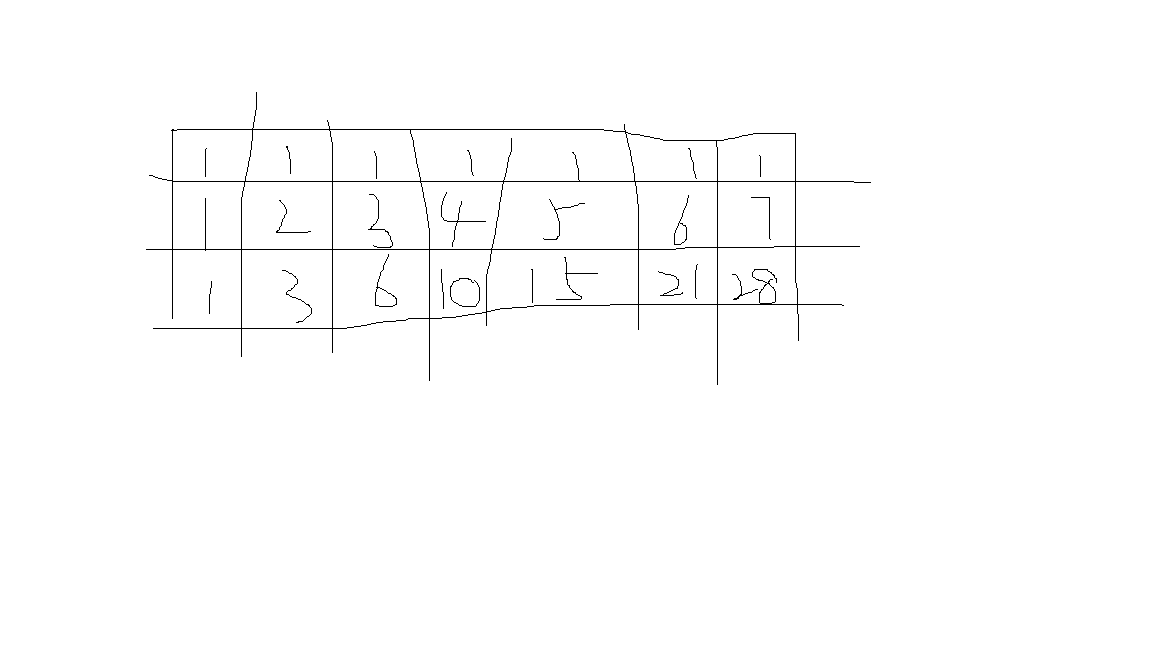

最靠边上的路径数都是1，然后他们旁边格子的路径数等于左边的格子加上上边的格子。

java代码

class Solution {
    public int uniquePaths(int m, int n) {
        int[][] dp = new int[m][n];        
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (i == 0 || j == 0)
                    dp[i][j] = 1;
                else {
                    dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
                }
            }
        }
        return dp[m - 1][n - 1];        
    }
}